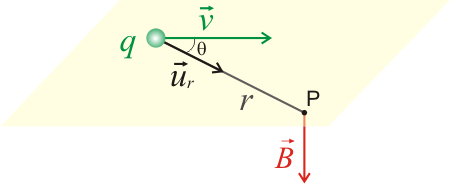
La inversión

La Inversión en Dibujo Técnico es una transformación geométrica en la que a una figura corresponde otra y en la que se cumple que:

• Dos puntos inversos (A, A’) están alineados con un punto fijo llamado Centro de Inversión (O),
• El producto de la distancia de un punto al Centro de Inversión por la distancia de su inverso al Centro de Inversión es constante (K) y se llama Potencia de Inversión.

Esto quiere decir que OA·OA’ = OB·OB’ = OT·OT = K

Trazando sucesivas rectas secantes a esta circunferencia encontramos más puntos y sus inversos. Puesto que K es constante, cuanto mayor sea OA, menor será OA’, es decir, cuando más alejado esté un punto A del Centro O, más cerca estará su inverso A’ del Centro O.

Existe una distancia para la cual un punto A y su inverso son iguales.

Lo puedes ver en el dibujo anterior. Se trata del punto de tangencia. El punto T coincide con su inverso y para él también se cumple que

OT·OT = K

Por tanto,

OT = Raíz cuadrada de K

Todos los puntos situados a la misma distancia del centro de inversión que este punto T son dobles. A este Lugar Geométrico se le llama Circunferencia de Puntos Dobles (CPD)

CIRCUNFERENCIA DE PUNTOS DOBLES O CIRCUNFERENCIA DE AUTOINVERSIÓN

La Circunferencia de Puntos Dobles (o circunferencia de Autoinversión) es el Lugar Geométrico de los puntos del plano que tienen sus inversos en sí mismos. Estos puntos equidistan del Centro de Inversión una distancia igual a la raíz cuadrada de la Potencia de Inversión K.

CÓMO DIBUJAR LA CIRCUNFERENCIA DE PUNTOS DOBLES

En realidad es muy sencillo. Dibuja una circunferencia que contenga dos puntos inversos A-A’ y dibuja la recta tangente a dicha circunferencia desde el Centro de Inversión. Esto determinará un punto de Tangencia.

La circunferencia con centro en O y radio O-T es la Circunferencia de Puntos Dobles.

En el dibujo anterior está muy claro.

CARACTERÍSTICAS DE LA INVERSIÓN

1. Dos pares de puntos inversos no alineados forman siempre una circunferencia

2. Dados dos puntos A, B y sus inversos A’, B’, las rectas A-A’ y B-B’ son antiparalelas de las rectas A-B y A’-B’

Esto quiere decir que el ángulo que forma la recta A-A’ con A’-B’ y con A-B son iguales que los que forma la recta B-B’ con A-B y con A’-B’ respectivamente.

3. Si K>0, la Inversión es positiva. Si K<0, es negativa y en este último caso la Inversión no tiene puntos dobles.

DETERMINAR UNA INVERSIÓN

Una Inversión puede venir determinada de 3 maneras diferentes:

1. Dado el Centro de Inversión y un par de puntos inversos
2. Dado el Centro de Inversión y la Potencia de Inversión
3. Dados dos pares de puntos inversos no alineados.

Veamos a continuación cada uno de los casos.

1. Dado el Centro de Inversión O y un par de puntos inversos A, A’, determinar el punto inverso de B.

Dibuja la circunferencia que pasa por A, A’ y B. Para ello traza las mediatrices de los segmentos A-A’ y A-B. El punto de intersección es el centro de la circunferencia que buscamos. Une B con el Centro de Inversión y obtendrás B’.

2. Dado el Centro de Inversión O y el valor de la inversión OT, determinar el punto inverso de A

Dibuja una circunferencia de radio OT con centro en el Centro de Inversión. Esta es la Circunferencia de Puntos Dobles. Toma un punto T cualquiera de la circunferencia. Dibuja la mediatriz del segmento A-T y la tangente a la circunferencia por T. En la intersección de ambas rectas se encuentra el centro C de una circunferencia de radio C-T que contiene el inverso de A. Une O con A para encontrarlo.

3. Dados dos pares de puntos inversos A, A’ y B, B’, determinar el punto inverso de D.

En la intersección de las rectas A-A’ con B-B’ se encuentra el Centro de Inversión. Dibuja la circunferencia que pasa por los puntos A, A’ y D. Une O con D y obtendrás D’ sobre dicha circunferencia.

LOS 5 CASOS DE INVERSIÓN

A continuación conocerás los 5 casos posibles de inversión. Estos los podrás aplicar a cualquier problema que se te presente.

1. La inversa de una recta que pasa por el Centro de Inversión es ella misma

¡Ojo! Esto no significa que cada punto sea inverso de sí mismo. Esto sólo ocurre en los puntos pertenecientes a la Circunferencia de Puntos Dobles.

Significa que un punto contenido en esa recta tendrá su inverso en la misma recta.

¿Cómo obtener, en este caso, el punto inverso?

Dados un Centro de Inversión O, un par de puntos inversos A, A’ y un punto B,

1. Toma un punto C aleatorio que no pertenezca a la recta y dibuja la circunferencia que contiene a A, A’ y C. Por la propiedad de que dos pares de puntos inversos siempre forman una circunferencia, podemos asegurar C’ estará en esta circunferencia.
2. Dibuja la circunferencia que pasa por C, C’ y B. En el punto de corte de esta circunferencia con la recta A-A’ se encuentra B’

(He borrado los trazados auxiliares para evitar confusiones en el dibujo. Como sabes, el centro de la circunferencia que pasa por tres puntos está en la intersección de las mediatrices de dos de los segmentos que unen dichos puntos)

2. La inversa de una recta que no pasa por el Centro de Inversión es una circunferencia que sí pasa por el Centro de Inversión.

Se cumple además que la recta que une el Centro de Inversión con el centro de la circunferencia es perpendicular a la recta dada.

Dados el Centro de Inversión O, un par de puntos inversos A, A’ y una recta r,

1. Dibuja la recta perpendicular a la dada que pase por el Centro de Inversión. Sobre esta recta se encontrará el centro.
2. Toma un punto cualquiera B de la recta y encuentra su inverso B’, haciendo pasar una circunferencia por A, A’ y B.
3. Dibuja la mediatriz de O-B’, ya que la circunferencia debe pasar por ambos puntos. Esta determinará el centro de la circunferencia inversa de r, cuyo radio será O-B’

3. La inversa de una circunferencia que pasa por el Centro de Inversión es una recta que no pasa por el Centro de Inversión

Este es el caso complementario del anterior. Dados un Centro de Inversión, un par de puntos inversos y una circunferencia, la recta inversa que buscamos será perpendicular a la recta O-C. Por tanto, dibuja la recta O-C y su perpendicular por el punto A’.

4. La inversa de una circunferencia que no pasa por el Centro de Inversión es otra circunferencia homotética de la primera.

Dados el Centro de Inversión, un par de puntos inversos y una circunferencia

1. Une el centro de la circunferencia con el Centro de Inversión. Sobre esta recta estará el centro de la circunferencia inversa.
2. Dibuja ahora la recta tangente a la circunferencia desde el Centro de Inversión. Como sabes, tienes que dibujar la mediatriz del segmento O-C y desde el punto medio M trazar un arco de circunferencia con radio M-O. Los puntos de corte determinan los puntos de tangencia T.
3. Halla el inverso T’ del punto de tangencia T. Este se encontrará en la circunferencia que pasa por T, A y A’.
4. Por el punto T’, pasa una perpendicular a la recta O-T y estó definirá el centro de la circunferencia inversa.

5. La inversa de una circunferencia que pasa por un par de puntos inversos es inversa de sí misma.

¡Atención! Cada punto de la circunferencia no es inverso de sí mismo, sino que cada punto de la circunferencia tiene su inverso sobre la propia circunferencia.

Esto se basa en la 1ª característica de la Inversión que he enunciado más arriba: Dos pares de puntos inversos no alineados forman siempre una circunferencia.

Fuente :

• https://www.10endibujo.com/inversion/

Campo magnético

El campo magnético B es una magnitud vectorial. Puede estar producido por una carga puntual en movimiento o por un conjunto de cargas en movimiento, es decir, por una corriente eléctrica.

La unidad de campo magnético en el Sistema Internacional es el tesla (T). Un tesla se define como el campo magnético que ejerce una fuerza de 1 N (newton) sobre una carga de 1 C (culombio) que se mueve a velocidad de 1 m/s dentro del campo y perpendicularmente a las líneas de campo.

El tesla es una unidad muy grande, por lo que a veces se emplea como unidad de campo magnético el gauss (G) que, aunque no pertecece al Sistema Internacional sino al sistema CGS, tiene un valor más acorde con el orden de magnitud de los campos magnéticos que habitualmente se manejan.

1 T = 10.000 gauss

Campo magnético creado por una carga puntual

Cuando una carga q se mueve con una cierta velocidad, como se muestra en la siguiente figura, crea un campo magnético en todo el espacio.

Dicho campo viene dado por la expresión:

Donde,

• q es la carga creadora del campo
• v es la velocidad de dicha carga
• r es la distancia desde el punto donde se encuentra la carga hasta el punto Pdonde se está calculando el campo
• u_r es un vector unitario que va desde el punto donde se encuentra la carga hacia el punto donde se calcula el campo
• μ₀ es una constante denominada permeabilidad del espacio libre. Su valor en el Sistema Internacional es μ₀ = 4π 10^-7 T m/A

La dirección y el sentido del campo B vienen dados por la regla de la mano derecha, y su módulo es el módulo del producto vectorial:

Dirección y sentidoMódulo

Cuando la carga q es negativa, el sentido de B es opuesto al que se muestra en la figura. El campo magnético en la dirección del movimiento es nulo, ya que en este caso los vectores v y u_r son paralelos y su producto vectorial es cero.

Fuente :

• https://www2.montes.upm.es/dptos/digfa/cfisica/magnet/campomag.html

Los vectores

Te explicamos qué es un vector en física y matemáticas, su sentido, tipos, características y ejemplos. Además, otras acepciones de vector.

Los vectores pueden representarse en el plano cartesiano con coordenadas x,y.

¿Qué es un vector?

En física y matemáticas, un vector es un segmento de una línea recta, dotado de un sentido, es decir, orientado dentro de un plano euclidiano bidimensional o tridimensional. O lo que es lo mismo: un vector es un elemento en un espacio vectorial.

Los vectores permiten representar magnitudes físicas dotadas no sólo de intensidad, sino de dirección, como es el caso de la fuerza, la velocidad o el desplazamiento. Ese rasgo de contar con dirección es el que distingue a las magnitudes vectoriales de las escalares.

Además, un vector puede representarse en un plano cartesiano mediante un conjunto de coordenadas (x,y), o en uno tridimensional (x,y,z). Los vectores se representan típicamente mediante una flecha dibujada por encima del símbolo empleado.

Características de un vector

Los vectores, representados gráficamente, poseen las siguientes características:

• Dirección. Definida como la recta sobre la cual se traza el vector, continuada infinitamente en el espacio.
• Módulo o amplitud. La longitud gráfica que equivale, dentro de un plano, a la magnitud del vector expresada numéricamente.
• Sentido. Representado por la punta de la flecha que gráficamente representa al vector, indica el lugar geométrico hacia el cual se dirige el vector.
• Punto de aplicación. Correspondiente al lugar o punto geométrico en donde inicia el vector gráficamente.
• Nombre o denominación. Representado mediante una letra que acompaña al vector gráficamente representado, y que coincide con la magnitud que expresa o con la suma de los puntos de inicio y fin de su valor.

Sentido de un vector

El sentido de los vectores se representa gráficamente mediante una punta de flecha apuntando en alguna dirección. Esto representa hacia qué lado de la línea de acción (dirección) se dirige el vector, o sea, hacia dónde apunta.

El sentido es sumamente importante a la hora de expresar magnitudes vectoriales, ya que puede determinar el tipo de operación o cálculo que es posible realizar con las mismas.

Tipos de vectores

Según la ubicación de su punto de aplicación, los vectores se clasifican en:

• Vectores libres. Aquellos que no poseen un punto de aplicación particular.
• Vectores deslizantes. Aquellos cuyo punto de aplicación puede ser uno cualquiera a lo largo de la recta de aplicación.
• Vectores fijos o ligados. Aquellos que poseen un único y determinado punto de aplicación.

Sin embargo, también es posible clasificar los vectores según otros elementos, de la siguiente manera:

• Vectores angulares o concurrentes. Aquellos que forman ángulos respecto de sus líneas de acción o direcciones.
• Vectores opuestos. Aquellos que poseen igual magnitud pero sentido contrario.
• Vectores colineales. Aquellos que comparten recta de acción.
• Vectores paralelos. Aquellos cuyas líneas de acción sean, justamente, paralelas.
• Vectores coplanarios. Aquellos cuyas rectas de acción estén situadas en un mismo plano.

Ejemplos de vectores

Los vectores permiten representar las diferentes fuerzas que intervienen en un movimiento.

La física usa vectores en el plano cartesiano para representar la combinación de fuerzas.

Los vectores permiten representar fuerzas contrapuestas gracias a que señalan la dirección.

Los vectores pueden sumarse y restarse entre sí.

En el plano cartesiano, los vectores permiten hacer muchos otros cálculos.

Otras acepciones de “vector”

El término vector se emplea también en biología, con el sentido de “mecanismo de transmisión” de alguna enfermedad o agente infeccioso.

Por ejemplo, el mosquito puede ser vector que numerosas enfermedades que requieren necesariamente de la picada de este insecto para transmitirse al ser humano. Los vectores sirven involuntariamente para que el agente infeccioso madure y se esparza geográficamente o poblacionalmente.

Por otro lado, se habla de vector también en el ámbito de la navegación espacial, como sinónimo de “lanzadera”, o sea, el vehículo de lanzamiento espacial que permite a otros vehículos más chicos alcanzar el espacio exterior.

Fuente:

• https://concepto.de/vector/